در این مقاله خواهیم آموخت:
- آزمون T مستقل و آزمون ناپارامتری متناظر آن
- آزمون T زوجی و آزمون ناپارامتری متناظر آن
- آزمون آنالیز واریانس 1 طرفه و انواع آن
- آزمون تحلیل واریانس اندازه مکرر
در مقاله قبلی با آزمون One Sample T Test و پیش فرضهای آن آشنا شدیم. گاهی در پژوهشی که در حال انجام آن هستیم، قصد داریم بدانیم که میانگین یک متغیر در دو گروه به چه صورت است؟ به عبارتی میخواهیم بدانیم که دو گروه از میانگین یکسانی برخوردار هستند و یا بین آنها تفاوت وجود دارد. برای مثال: میخواهیم میانگین قد را در دو گروه دختر و پسر مقایسه بکنیم. در این صورت از آزمون T Independent (مستقل) استقاده میکنیم.
پیش فرضهای آزمون تی مستقل:
- مقادیر دو متغیر باید مستقل و از دو جامعه (دختر/ پسر) باشند.
- مقیاس متغیر وابسته ( قد) باید کمی و در سطح فاصلهای/ نسبی باشد.
- مقیاس متغیر مستقل (جنسیت) باید کیفی و در سطح اسمی باشد.
- توزیع دادههای متغیر وابسته (متغیر قد) باید بصورت نرمال باشد. چنانچه از توزیع نرمال تبعیت نکند باید از معادل ناپارامتری آن یعنی تست من ویتنی Mann Whitney استفاده کرد.
در مثال بالا فرضیه مورد تحقیق به شکل زیر خواهد بود:
که میانگین قد در جامعه دختران است و
میانگین قد در جامعه پسران است. فرضهای بالا را میتوان به شکلی دیگر نیز نوشت:
اگر فرضیه بالا را در سطح اطمینان 95 درصدی مورد آزمایش قرار دهیم، درصورتیکه مقدار P value از 0.05 کمتر باشد، فرض صفر رد میشود؛ به این معنیکه اختلاف معناداری بین میانگین قد در دو جمعیت دختر و پسر وجود دارد. بطورکلی هرچه مقدار آماره آزمون (t) زیاد باشد و از صفر فاصله بگیرد، احتمال رد فرض بیشتر میشود.
همانطور که قبلا هم اشاره شد برای تصمیمگیری درمورد رد و یا پذیرش فرضیه میتوان از فاصله اطمینان نیز کمک گرفت. درصورتیکه در این بازه عدد صفر قرار بگیرد (به عبارت دیگر: علامت کران بالا، مثبت و علامت کران پایین، منفی باشد) به این معنی است که اختلاف میانگین بین دو گروه میتواند عدد صفر را اختیار کند، پس فرض صفر را میپذیریم. اما درصورتیکه در این بازه، عدد صفر قرار نگیرد، فرض صفر را رد میکنیم.
مسیر اجرای آزمون t مستقل در SPSS:
Analyze → Compare Mean → Independent Samples T Test
مسیر اجرای آزمون Mann Whitney در SPSS:
Analyze → Non-Parametric Test → Legacy Dialogs → 2 Independent
آزمون دیگری که برای بررسی یک متغیر کمی در جمعیتهای مستقل بکار میرود آزمون تحلیل واریانس یک طرفه One Way ANOVA است. با این تفاوت که برای مقایسه متغیر در بیش از 2 گروه مورد استفاده قرار میگیرد. درواقع در آزمون تی مستقل دو گروه مستقل وجود داشت و هدف محقق، مقایسه میانگین یک صفت کمی در این دو گروه بود. حال تصور کنید که با یک صفت کیفی روبرو هستیم که تعداد رده های آن بیش از دو حالت است و هدف محقق، مقایسه میانگین یک صفت کمی در این گروه ها باشد. برای مثال قصد داریم میانگین IQ را در 3 گروه زیر لیسانس، لیسانس و تحصیلات تکمیلی مقایسه کنیم. در این صورت از آنجایی که با k (k>2) گروه سروکار داریم، دیگر به سراغ آزمون t مستقل نمیرویم.
آنالیز واریانس تحت رویکردهای مختلفی همچون آنالیز واریانس یک طرفه، دو طرفه، سه طرفه و چند طرفه قابل استفاده است. چنانچه فقط یک متغیر کیفی وجود داشته باشد، به منظور مقایسه میانگین متغیر کمی در سطوح آن از آنالیز واریانس یک طرفه استفاده می شود. هرگاه دو متغیر کیفی وجود داشته باشد (مانند سطح تحصیلات و جنسیت) به منظور مقایسه میانگین متغیر کمی در ترکیب سطوح این دو متغیر از آنالیز واریانس دو طرفه استفاده می شود. به همین ترتیب با افزایش تعداد متغیرهای کیفی نوع آنالیز واریانس استفاده شده نیز تغییر خواهد کرد.
در این آزمون، یک شرط مهمی که حتما میبایست چک شود، شرط برابری واریانس در ردههای مختلف است. این شرط از طریق Levan Test قابل بررسی است و نرمافزار SPSS جدول برابری واریانس را برای ما نمایش میدهد. درواقع باید واریانس متغیر قد در 3 رده تحصیلی با هم برابر باشد. به سایر پیشفرضهای آزمون ANOVA در ادامه پرداختهشدهاست.
فرضیههای این آزمون در قالب زیر است:
: حداقل میانگین یکی از ردهها متفاوت باشد.
درصورتیکه P value محاسبهشده از مقدار کمتر باشد، فرض صفر رد میشود. به این معنیکه میانگین حداقل یکی از ردهها با دیگری متفاوت است.
در آنالیز واریانس، پس از رد شدن فرض صفر، برای مشخص شدن اینکه میانگین کدام گروه ها با یکدیگر تفاوت دارند از آزمون های تعقیبی (پسین Post Hoc Tests) استفاده می شود. در واقع به کمک این آزمون ها میانگین های گروه های مورد بررسی دو به دو با یکدیگر مقایسه می شوند تا مشخص شود میانگین کدام گروه ها یا کدام سطوح با یکدیگر اختلاف دارند. در محیط SPSS با علامت ستاره (*) اختلاف میانگینها در خروجی نشانه گذاری میشود.
در جداول پایین، انواع آزمونهای تعقیبی و وجه تمایز هریک از آنها آورده شده است:
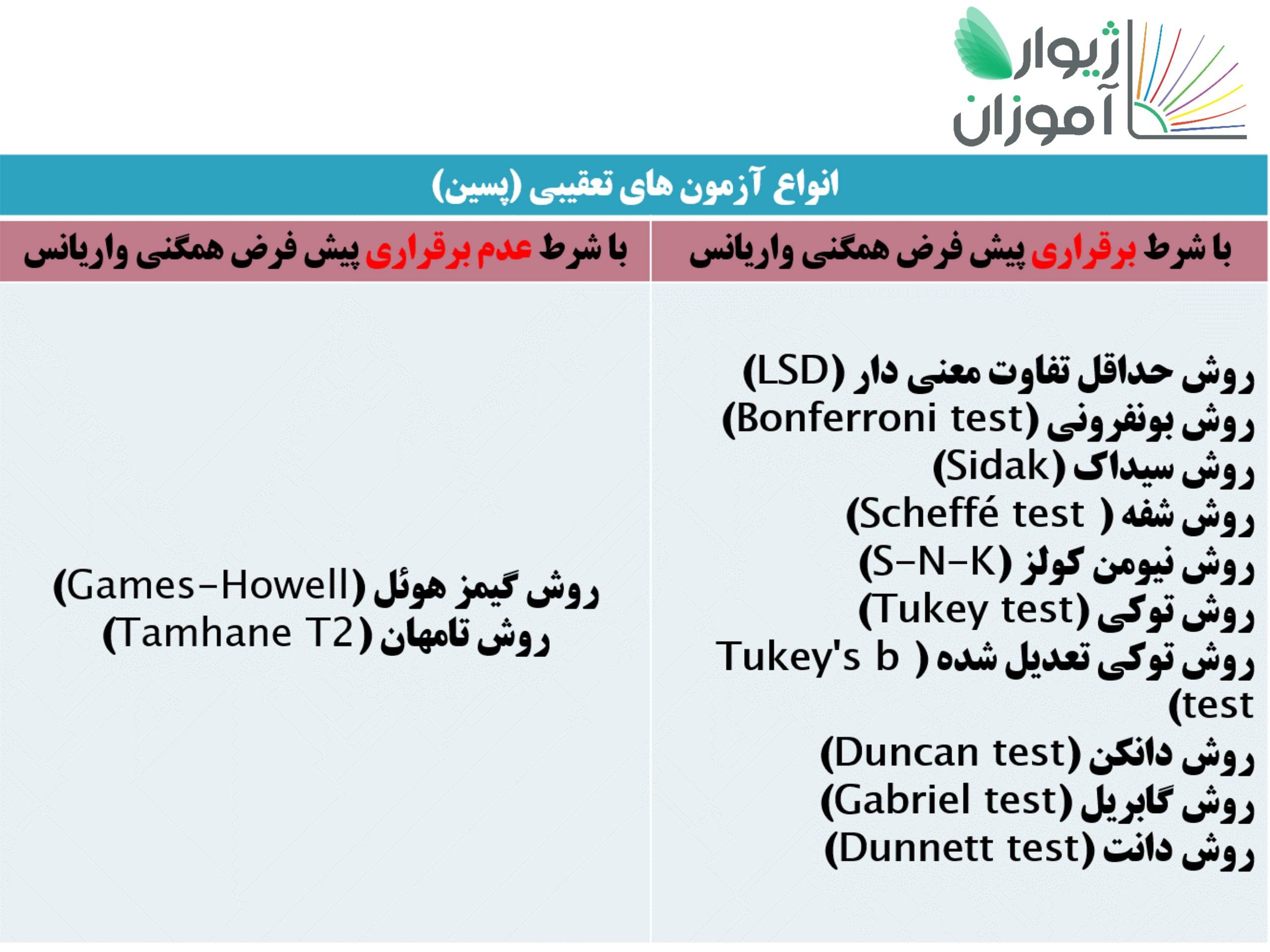

این آزمون نیز از پیش فرضهایی برخوردار میباشد که لازم است قبل از اجرای آن، مورد بررسی قرار گیرند.
پیش فرضهای آزمون آنالیز واریانس یک طرفه:
- نفرات در هر گروه بصورت تصادفی انتخاب شدهباشند و ردهها از همدیگر مستقل باشند.
- توزیع متغیر وابسته (متغیر پاسخ) در سطوح مختلف متغیر کمی، نرمال باشد.
- واریانس دادههای هر گروه برابر باشد، در واقع باید فرض همگونی واریانسها برقرار باشد.
بسته به پیش فرضهای گفتهشده، با یکی از سه حالت زیر مواجه میشویم که برای هر یک باید از آزمونی متناسب که داخل پرانتز آورده شدهاست استفاده کرد:
الف) توزیع متغیر کمی نرمال باشد و همگنی واریانس نیز برقرار باشد. (آزمون ANOVA)
ب) توزیع متغیر کمی نرمال باشد اما همگنی واریانس برقرار نباشد. (Welch یا Brown-Forsythe)
ج) توزیع متغیر کمی نرمال نباشد با هیچ تبدیلی هم امکان نرمال کردن آن فراهم نشود، یا در شرایطی باشیم که حجم نمونه در گروه های مورد بررسی خیلی کم باشد. (کراسکال والیس (معادل ناپارامتری ANOVA))
در نهایت اگر بخواهیم بر روی دادههای گردآوری شده، این آزمون را پیاده سازیم باید از مسیر زیر درفضای SPSS پیش برویم:
Analyze → Compare Mean → One Way Anova
اما در بعضی از مطالعات، بویژه پژوهشهای مداخلهای، قصد داریم تاثیر مداخله را بر روی یک گروه از افراد در دو زمان متفاوت (قبل از مداخله و بعد از مداخله) بررسی کنیم. بنابراین باید از آزمونی استفاده کنیم که تفاوت میانگینهای دو جمعیت وابسته (با یکدیگر جفت هستند) را میآزماید. آزمون مناسب در این نوع از مطالعات، آزمون تی زوجی Paired T Test است که هر فرد را دوبار در دو زمان متفاوت، مورد بررسی قرار میدهد.
برای مثال: قصد داریم تاثیر مصرف داروی X را بر روی فشارخون 30 بیمار بررسی کنیم. لازم است که میانگین فشارخون این 30 نفر را قبل از مصرف داروی X و پس از مصرف
همان دارو محاسبه و درنهایت مقایسه کنیم. اگر میانگین فشارخون، پس از مصرف داروی X کاهش یافته باشد؛ به معنی موثر بودن دارو است. اگر میانگین فشارخون، قبل و بعد از مصرف دارو تفاوت معنی داری نداشته باشد؛ بیاثر بودن داروی مصرفی را عنوان میکند.
برای مثال بالا میتوان به اینصورت فرضیههای مطالعه را نوشت:
در واقع اگر تفاضل این دو میانگین را با علامت (Different) نشان دهیم، میتوانیم به شکل دیگری نیز فرضیه این آزمون را بنویسیم:
حال تصور کنید که بخواهیم فرض گفته شده را در سطح 99 درصد بسنجیم. درصورتیکه P value از عدد 0.01 بیشتر باشد؛ فرض صفر را میپذیریم. درواقع مداخله صورت گرفته، تاثیری در کاهش میانگین فشارخون نداشته و مداخله موثر نبوده است. اگر در فاصله اطمینانی که برای آماره T وجود دارد، عدد صفر قرار بگیرد نیز همین استنباط را خواهیم کرد. در نهایت اگر مقدار عددی آماره T آزمون زوجی به صفر نزدیک باشد، فرض پذیرفته میشود و بالعکس.
پیش فرضهای آزمون تی زوجی:
- مقادیر دو متغیر باید وابسته (بر روی یک جمعیت) باشد.
- مقیاس متغیر وابسته ( فشارخون) باید کمی و در سطح فاصلهای/ نسبی باشد.
- توزیع دادههای متغیر وابسته (متغیر فشارخون) باید بصورت نرمال باشد. چنانچه از توزیع نرمال تبعیت نکند باید از معادل ناپارامتری آن یعنی تست ویل کاکسون علامتدار Wilcoxon signed-rank استفاده کرد.
**نکته مهمی که باید در نظر گرفت این است که تفاوت دو آزمون گفته شده در پیش فرض اول هر آزمون است.
مسیر اجرای آزمون T زوجی در فضای SPSS:
Analyze → Compare Mean → Paired Samples T Test
مسیر اجرای آزمون Wilcoxon signed-rank در فضای SPSS:
Analyze → Non-Parametric Test → Legacy Dialogs → 2 Related Samples
تصور کنید در یک پژوهش مداخلهای، محقق قصد دارد اثر یک دارو را از طریق مقایسه کارایی آن در گروه شاهد و گروه تحت درمان بسنجد اما گروه تحت درمان در این مطالعه، خود به 2 قسمت دیگر تبدیل شود و گروهی را 1 ماه بعد از دریافت درمان و گروه دیگری را 3 ماه پس از دریافت دارو مورد بررسی قرار دهد. در این صورت با بیش از دو گروه سروکار دارد. برای تحلیل نتایج این پژوهش باید از آزمونی که تعمیمیافته T زوجی است و برای بیش از دو گروه بکار میرود، یعنی Repeated measure (آزمون تحلیل واریانس با اندازهگیری های مکرر (تکرار شده)) استفاده کرد.
سخن پایانی
درک وجه تمایز آزمونهای گفتهشده، برای استفاده صحیح از آنها الزامی است. پس میبایست تمامی پیشفرضها در ابتدا چک شوند و درصورت برقرار بودن، آزمون موردنظر را بر روی دادهها اعمال کرد. در نمودار زیر بصورت خلاصه، مطالب این مقاله آوردهشدهاست:
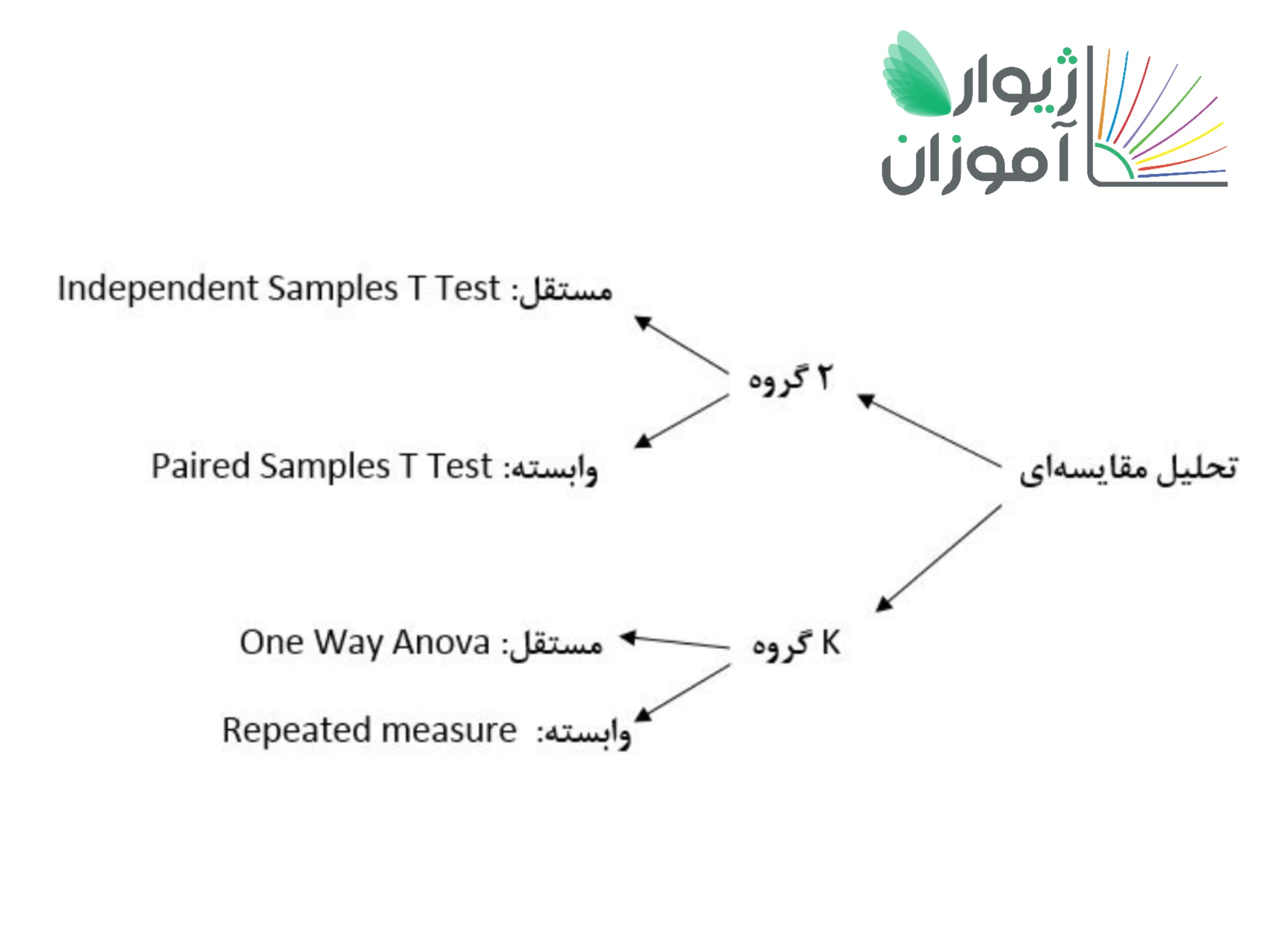
دانلود فایل PDF آزمونهای Tمستقل، Tزوجی و آزمونهای ناپارامتری متناظر آن








