مفهوم آزمون آماری
مفهوم خطای اول و دوم در آزمونهای فرض
انواع فرضیه
آزمون آماری برای معادل ناپرامتری آن
از مباحث مهم در آمار استنباطی، آزمونهای آماری هستند. قبل از اینکه وارد مبحث آزمونهای آماری بشویم لازم است تعدادی از مفاهیم مهم و پرکاربرد در این حوزه را بدانیم.
زمانی از آزمونهای آماری استفاده میکنیم که قصد داشته باشیم فرضی را در مورد جامعه مورد مطالعه بسنجیم؛ درحالی که تنها نمونهای از آن جامعه موردنظر داریم. بنابراین فرض مدنظر را برروی نمونه گرفته شده، بررسی میکنیم و با استفاده از مقادیر خطای اولیه و P value تصمیم به رد یا پذیرش فرض مربوطه میگیریم. بسته به نوع فرضیه آماری و سطح سنجش متغیرها، باید مناسبترین آزمون آماری را برای آزمودن فرضیه موردنظر خود انتخاب کنیم. در مقالات قبلی، دریافتیم که سطح سنجش متغیرها یا کیفی (اسمی/ رتبهای) و یا کمی (گسسته/ پیوسته) است.
در ادامه با مفهوم فرض اماری، انواع خطاهای اماری و P value آشنا میشویم.
فرضیه: گزارههایی هستند در مورد پارامتر جامعه که به بیان رابطه بین دو متغیر، تاثیر یک متغیر بر دیگری و نیز مقایسه یک متغیر در بین یک یا چندگروه میپردازد. بنابراین در تحقیق، 3 دسته فرضیه رابطهای، تفاوتی و علی وجود دارد.

فرضیه رابطهای Relational Hypothesis : همواره با دو متغیر سروکار دارد و کیفیت ارتباط بین این دو متغیر را میسنجد. این نوع فرضیه سعی در اثبات علی بودن ارتباط ندارد.
فرضیه علیتی Causal Hypothesis : در این نوع از فرضیه، هدف پژوهشگر صرفا تعیین ارتباط و همبستگی دو یا چند متغیر نیست. بلکه قصددارد رابطهای عمیقتر را بررسی کند و به رابطه علت و معلولی برسد. درواقع بگوید یک متغیر علت متغیر دیگری است. اصولا برای بررسی این دسته از فرضیهها از ازمونهای رگرسیون استفاده باید کرد.
فرضیه تفاوتی Differential Hypothesis: در این نوع فرضیه، بدنبال بررسی و مقایسه تفاوت اثر دو یا چند متغیر بر یک یا چند متغیر دیگر هستیم. فرضیههای تفاوتی خود به دو دسته کلی تقسیم میشوند:
الف) گاه در این فرضیهها هدف ما مقایسه پارامتر جامعه با یک مقدار مفروض است که در ادامه در همین مقاله مورد بررسی قرار خواهد گرفت.
ب) گاه هدف ما مقایسه میانگین یک متغیر در دو گروه یا چند گروه است، یا مقایسه میانگین یک متغیر در یک گروه اما در دو زمان مختلف.
بطورکلی، فرضیه آماری مبنای انتخاب روشهای آماری بوده است که در طبقه بندی دیگری میتوان آن را به دو دسته تقسیم کرد:

الف) فرض صفر: این فرض را با نماد نشان میدهند و اصولا عدم تاثیر یک متغیر بر متغیر دیگر را عنوان میکند. همچنین در مواردی فرض صفر، عدم تفاوت یک متغیر در بین 2 یا چند گروه و عدم ارتباط بین متغیرهارا بیان میکند. در یک مطالعه، هدف ما آزمودن این فرض است تا در نهایت آن را رد و یا تایید کنیم.
ب) فرضیه بدیل: فرضیه مخالف فرض صفر است که آن را با نماد نشان میدهند و اصولا این فرض، بیانگر انتظار پژوهشگر از نتایج پژوهش است.
در تقسیم بندی دیگری میتوان گفت دو نوع فرضیه کلی داریم:
فرضیه یک طرفه: فرضیهای است که برای رد آن، صرفا یک حالت وجود دارد.
فرضیه دو طرفه: فرضیهای است که میتوان 2 حالت را برای رد در نظر داشت.
: فرضیه دو طرفه (در صورتی که میانگین از 20 کمتر یا بیشتر باشد، فرض صفر رد میشود.)
: فرضیه یک طرفه
: فرضیه یک طرفه
نکتهای که باید مورد توجه قرار داد این است که همیشه در انجام آزمونهای آماری نمیتوانیم 100 درصد از کار خود اطمینان داشته باشیم و محقق میتواند در خصوص بررسی ارتباط بین دو متغیر یا بررسی یک متغیر در دو گروه، دچار خطا شود. در دنیای پژوهش با دو نوع خطای مهم مواجه هستیم که در ادامه به توضیح هر یک میپردازیم:
الف) خطای نوع اول: احتمال رد فرض ، درحالیکه درست بوده است. در واقع این نوع خطا زمانی اتفاق میافتد که محقق وجود رابطه بین دو متغیر را میپذیرد درحالیکه در حقیقت رابطهای بین آن دو متغیر وجود ندارد. احتمال ارتکاب خطای نوع اول را آلفا
مینامند. همچنین آن را به نام سطح معنی داری نیز میشناسند. تعیین مقدار خطای نوع اول برعهده پزوهشگر است و پیش از انجام آزمون، آن را مشخص میکند. در صورتی که مقدار را از عدد 1 کم بکنیم
به سطح اطمینان آزمون دست مییابیم.
برای مثال اگر آزمونی با سطح خطای 5 درصد انجام شود یعنی تا 95 درصد اطمینان داریم که فرض را بهدرستی پذیرفتهایم.
ب) خطای نوع دوم: به احتمال پذیرش فرض در حالی که فرض صحیحی نبوده است گفته میشود. خطای نوع دوم را با نماد
نشان میدهند و حاصل تفاضل آن از عدد 1
را توان آزمون یا Power مینامند.
خطای نوع اول و دوم در تعیین حجم نمونه و همچنین رد یا پذیرش فرض صفر، تاثیر بسزایی دارد. به این صورت که برای کاهش هر دو خطا باید حجم نمونه بیشتری را اتخاذ کرد.
از مفاهیم پایه در مبحث آزمون آماری گذر کنیم و به سادهترین آزمون آماری یعنی آزمون t تک نمونهای بپردازیم.

زمانی که قصد داشته باشیم میانگین یک جامعه را با یک مقدار نظری مقایسه کنیم از آزمون آماری پارامتری T تک نمونه (One Sample T test) یا معادل ناپارامتری آن، آزمون نشانه (Sign)، استفاده میکنیم. این مقدار فرضی میتواند یک مقدار رایج معمول، یک مقدار مورد انتظار و یا یک مقدار استاندارد باشد.
در آزمون T تک نمونه ای، با نمونهای از جامعه مورد نظر سروکار داریم و قصد داریم ابتدا فرض مورد نظر را در نمونه گرفته شده بسنجیم و نتیجه آن را به جامعه تعمیم بدهیم.
برای مثال، قصد داریم آزمون کنیم که میانگین وزن دانش آموزان یک مدرسه، 55 کیلوگرم است یا خیر؟
مقدار مفروض در این سوال عدد 55 است و قصد داریم میانگین جامعه را با این مقدار نظری بسنجیم.
تصور کنید طبق این سوال، فرض ما این است که میانگین وزن دانشآموزان برابر 55 است و مخالف این فرض را در قسمت مینویسیم.
به فرضیههای پایین، توجه بکنید:
** «علامت مساوی همواره باید در فرض H صفر وارد شود.»
بطور کلی، محقق با سنجش فرضیه صفر به این نتیجه میرسد که فرض موردنظرش صحیح بوده است و یا خیر.
چگونه میتوان به رد فرض و یا پذیرش آن پی برد؟
همانطور که ابتدای مقاله نیز اشاره شد، در زمان شروع مطالعه، محقق تصمیم میگیرد که با سطح خطای 0.05 مطالعه خود را پیش ببرد. به این معنی که با احتمال 95 درصد مطمئن هستیم که فرض صحیح را میپذیریم و تنها 0.05 احتمال دارد به اشتباه فرض
درست را رد کنیم
و مرتکب خطا شویم. مسلم است که ما نمیخواهیم فرض
درست را به اشتباه رد کنیم و بدنبال کاهش خطا هستم.
اگر محقق بخواهد پژوهش خود را با اطمینان بالایی پیش ببرد باید درصد کمتری را به خطا اختصاص دهد، که البته حجم نمونه بالا را در این مواقع به همراه دارد. در هر صورت، محقق و مشاور آماری در ابتدای پژوهش، بسته به اهدافی که در سر دارند حداکثر مقداری را برای خطای نوع اول در نظر میگیرند. این مقدار به طور معمول، میتواند 0.01 ، 0.05 یا 0.1 باشد که اصولا حد وسط یعنی مقدار 5 درصد، مقدار مناسبی برای احتمال ارتکاب این خطا است.
همچنین در همه ازمونهای آماری، یکی از مقادیر مهمی که در جداول نهایی گزارش میشود، P value (معنی داری Significant) است. با استفاده از این عدد و مقایسه مقدار آن با α میتوان تصمیم به رد و یا پذیرش فرضیه گرفت. مقدار P value اگر کمتر از درصد خطایی باشد که در ابتدا درنظر گرفتیم؛ فرض رد میشود و اگر از حداکثر درصد خطا
بیشتر باشد آن را میپذیریم.
در یک قاعده کلی داریم:
رد فرض
P value
پذیرش فرض
P value
در تفسیر دو حالت بالا میتوان گفت: حداکثر مقداری است که برای خطا در نظر گرفتهایم، هر مقدار خطایی تا این حد معقول است و فرض ما را رد میکند، در واقع اگر
باشد یعنی تا 5 بار از 100 بار انجام یک آزمایش، حق ارتکاب این خطا را داریم اما درصد خطایی بالاتر از آن را اگر مرتکب شدیم، فرض
را رد نمیکنیم و میپذیریم.
نکته مهم دیگر که باید به آن دقت کرد 1 طرفه یا 2 طرفه بودن فرضیه مدنظر است که بالاتر به آن اشاره شد.
- درتمامی آزمونهای آماری قواعد بالا صادق است.
تصویر پائین، ناحیه رد و پذیرش را در یک فرضیه دو طرفه، نشان میدهد.
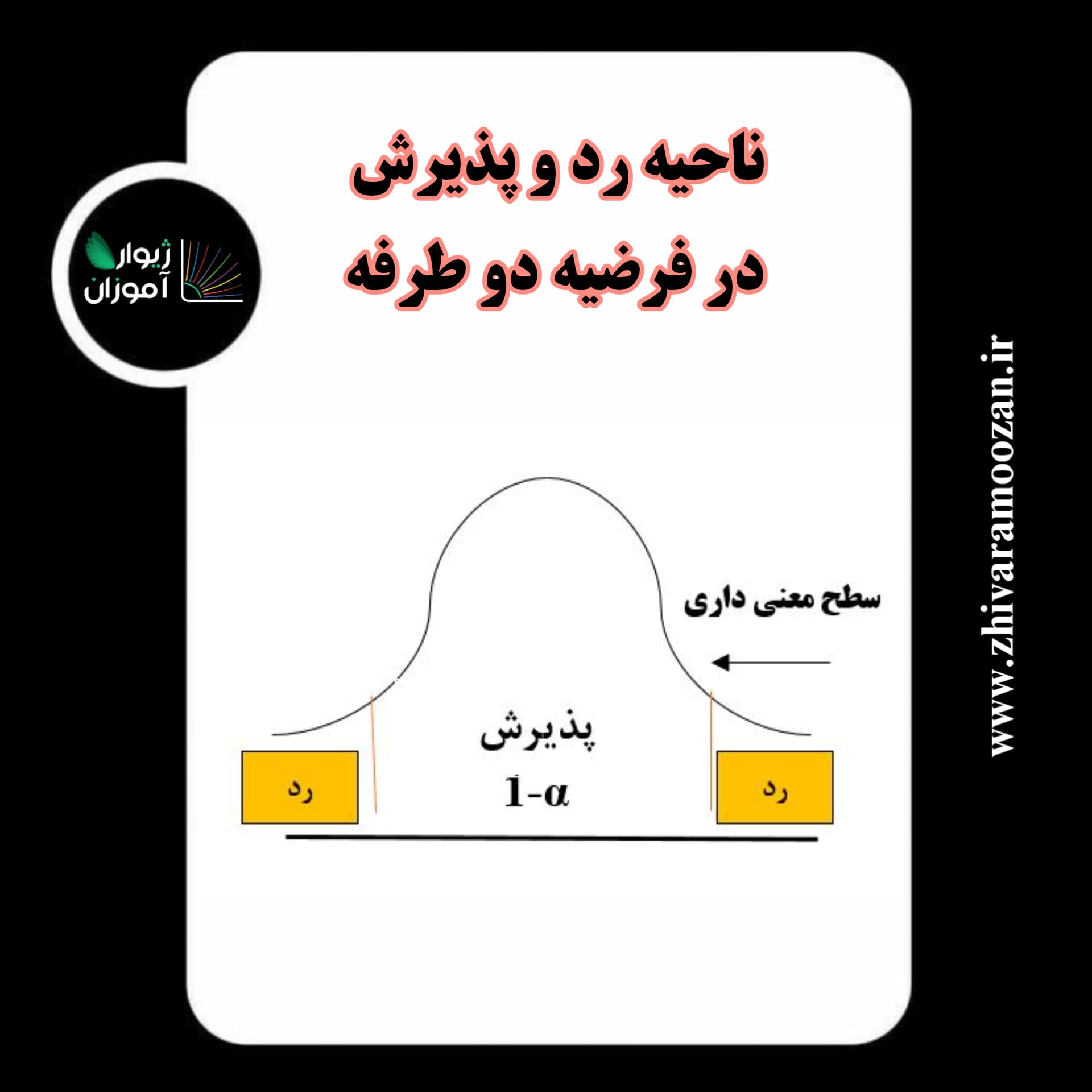
پس از آشنایی با مقدمات اولیه، به سراغ پیشفرضهای آزمون One Sample T Test میرویم:
- در این آزمون، حتما باید متغیر مورد بررسی کمی باشد (چه در سطح سنجش فاصلهای و چه نسبی)
- از آنجایی که از آزمون پارامتری استفاده میکنیم باید توزیع متغیر موردنظر نرمال باشد. چنانچه نرمال نباشد از معادل ناپارامتری آن استفاده میکنیم که جلوتر به آن اشاره خواهیم کرد.
- باید مقداری نظری را برای میانگین جامعه درنظر داشته باشیم تا بتوانیم فرضیه خود را با این آزمون بسنجیم.
همانطور که گفته شد پس از انجام آزمون بر روی دادهها، برای تفسیر نتیجه آن، در ابتدا P value را بررسی میکنیم و تصمیم میگیریم که فرض صفر را رد کنیم یا بپذیریم. علاوه بر این میتوان از فاصله اطمینان در آزمونهای t برای تفسیر نتیجه و تصمیمگیری در مورد رد و یا پذیرش فرضیه مدنظر استفاده کرد. به این صورت که با توجه به علامت مقادیر حد بالا و حد پایین این فاصله میتوان گفت:
- هرگاه حد پائین و بالا مثبت باشد، میانگین حقیقی از مقدار مورد فرض بزرگتر است و تفاوت میانگینها معنی دار است. (رد فرض صفر)
- هرگاه حد پائین و بالا منفی باشد، میانگین حقیقی از مقدار مفروض کوچکتر است و اختلاف معنی داری مشاهده میشود (رد فرض صفر)
- هرگاه حد پائینی منفی و علامت حد بالایی مثبت باشد، میانگین با مقدار مفروض برابر است و اختلاف معنیداری مشاهده نمیشود. (پذیرش فرضیه صفر)
لازم به ذکر است که مبنای اصلی آزمون های T (تک نمونه و یا مستقل) اختلاف میانگین ها است. در T تک نمونهای بجای مقدار مفروض را قرار میدهیم.
به فرمول پائین، دقت کنید:
- مقدار این تفاضل با سطح معنی داری رابطه عکس دارد یعنی هرچه تفاوت بین دو میانگین بیشتر باشد، سطح معنی داری از ۵صدم کوچکتر میشود (رد فرض صفر)
- یک رابطه مستقیم بین مقدار آماره آزمون (t) و اختلاف بین میانگین ها وجود دارد، درواقع هرچه این اختلاف بیشتر باشد مقدار t بیشتر است. (طبق فرمول بالا تفاضل در صورت کسر قرار دارد، بنابراین رابطه مستقیم دارد)
برای انجام این آزمون در فضای SPSS، از مسیر Analyze → Compare Mean→ One Sample T میتوان آزمون مربوطه را اجرا کرد و در صورتیکه در میان پیشفرضهای گفته شده برای این آزمون، پیش فرض دوم برقرار نباشد (یعنی توزیع متغیر ما از توزیع نرمال تبعیت نکند) ابتدا سعی به نرمال کردن دادهها از منوی Transform میکنیم و در صورتی که دادهها نرمال نمیشدند از مسیر Analyze → Non-Parametric Test → Legacy Dialog 2Related Samples آزمون ناپارامتری Sign را انتخاب میکنیم.
سخن پایانی
برای وارد شدن به مبحث آمار استباطی و فهم آزمونهای آماری، لازم است بر مفاهیم آماری اولیه، نظیر P value و …. تسلط کافی یافت، سپس با مجموعهای از دیتا، این آزمون را از مسیر گفتهشده در نرمافزار SPSS اجرا کرد تا در ذهن تثبیت شود. برای یادگیری صفر تا صد نرم افزار spss و انجام کارهای آماری پژوهشهای خودتان توصیه ما به شما شرکت دردوره صفر تا صد spss برای پژوهشگراناست. برای اطلاعات بیشتر و شرکت در این دوره با گارانتی یک ماهه بازگشت وجه درصورت هرگونه نارضایتی اینجا کلیککنید.








